Keine Panik! Wir haben Dir die ultimative Checkliste erstellt, die bundeslandspezifisch alle relevanten Themen zusammenfasst!
So hast Du alles Wichtige auf einen Blick, um Dich optimal auf die Prüfung vorzubereiten – ohne böse Überraschungen oder Blackout-Gefahr!
Hast Du diese Liste, kannst Du Dir absolut sicher sein, dass Du nichts Wichtiges vergisst.
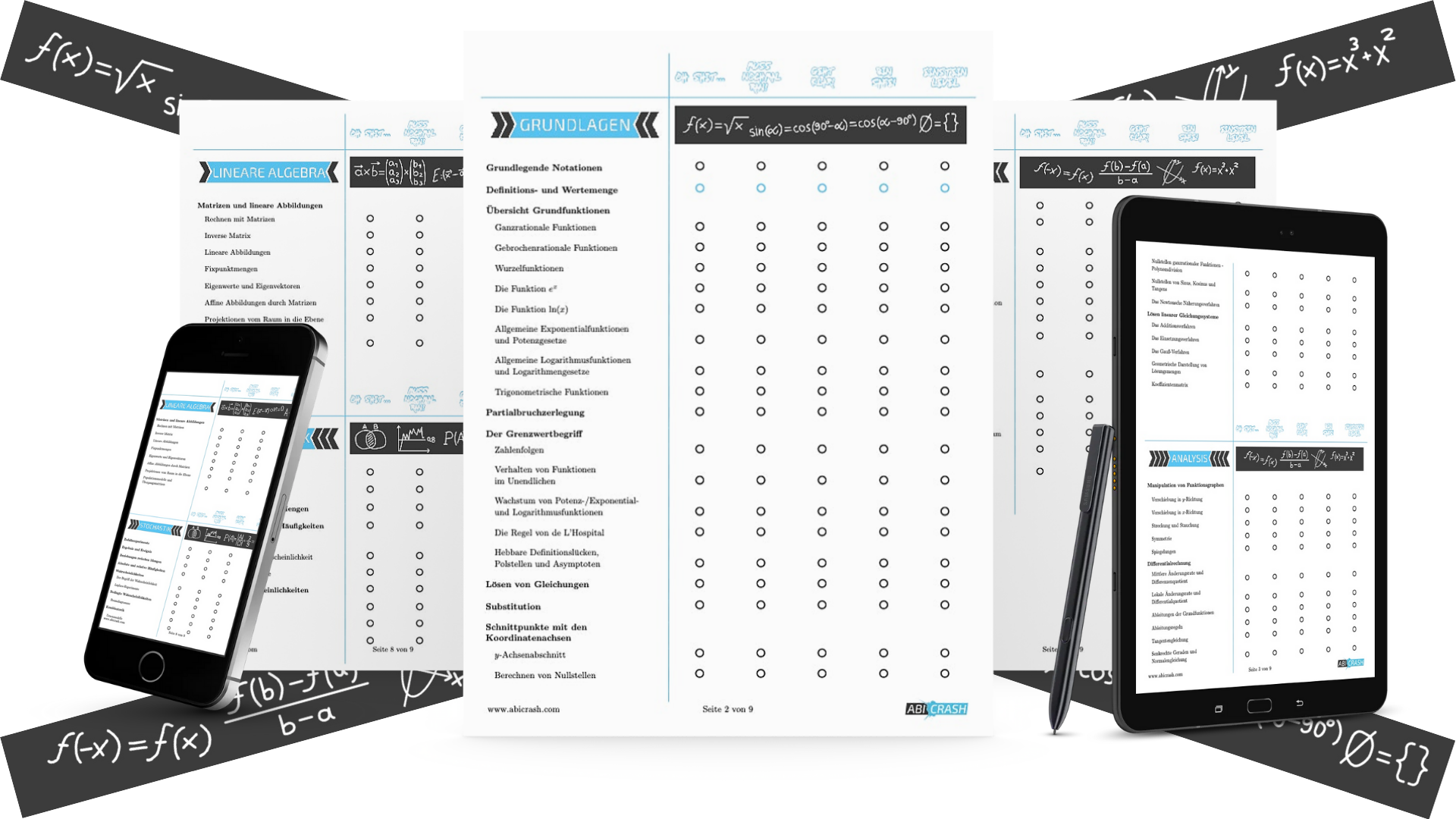
Unsere Checkliste ist unterteilt in die vier übergeordneten Bereiche Grundlagen, Analysis, Lineare Algebra und Stochastik. Übersichtlich aufgelistet werden alle Themen, die Du bis zur Abiturprüfung unbedingt üben solltest.
Bevor Du mit dem Lernen beginnst, kannst Du Dich in allen Themen selbst einschätzen und Deinen Lernfortschritt mit Hilfe unserer Skala überwachen.
Wir haben uns die Abituraufgaben der letzten Jahre angesehen und so herausgefunden, welche Themen immer wieder abgefragt wurden. So weißt Du, auf was Du Dich besonders konzentrieren solltest – vor allem wenn die Zeit knapp wird!
Weitere Hinweise, zum Beispiel Kürzungen des Lehrplans aufgrund der Corona-Pandemie oder spezielle Wahlbereiche, haben wir ebenfalls für Dich gekennzeichnet.
Mach Dir keine Sorgen, wenn am Anfang Deiner Lernsessions noch viele Kreuze auf der linken Seite stehen! Es ist nur wichtig, dass Du im Auge behältst, mit welchen Themen Du Dich intensiv vor den Prüfungen auseinandersetzen solltest.
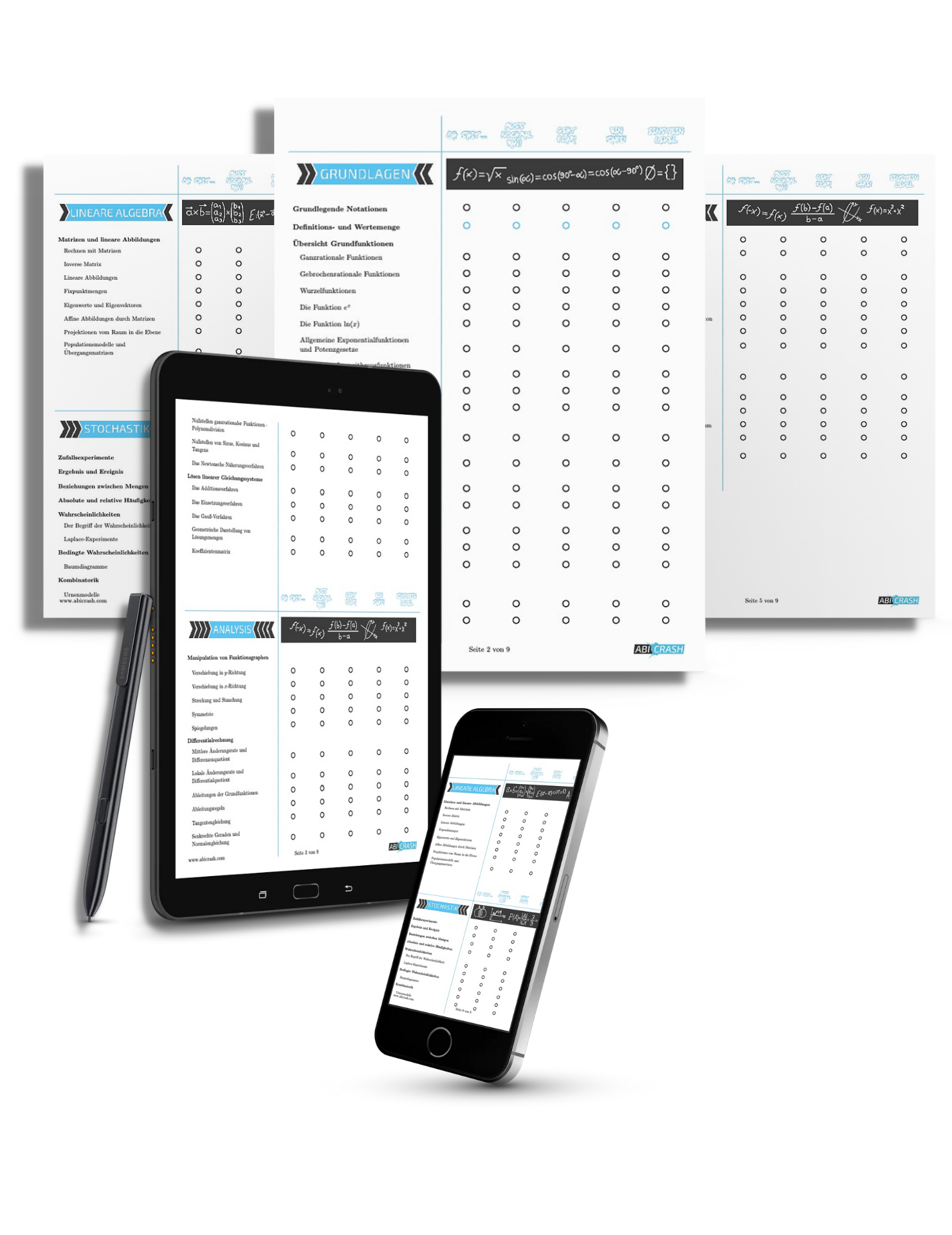
Wir haben für dich die ultimative Checkliste erstellt, die für die erfolgreiche Abiturvorbereitung im Fach Mathematik unumgänglich sind.

ABIcrash kommt zu dir nach Hause. Über 5.000 AbiturientInnen haben die gesamte Oberstufe Mathematik erfolgreich mit dem Kit bestanden und sich sicher auf das Abitur vorbereitet.

In der heißen Phase vor dem Abi zählt jeder Tag. Wiederhole und über alle Themen die für dein Abitur relevant sind in einem Kurs in deiner Nähe oder einem Live-Online-Format.






Die Checkliste bietet dir eine bundeslandspezifische Auflistung aller für dich relevanten Themen für dein Mathe-Abitur (auch nach Leistungsniveau getrennt).
Abiturrelevanten Themen in 2024 (Beispiel):
Lösen linearer Gleichungen (Additionsverfahren, Gleichsetzungsverfahren, Einsetzungsvefahren, Gauß-Verfahren)
Lösen quadratischer Gleichunen (Mitternachtsformell)
Lineare und Quadratische Ungleichungen
Potenz- und Logarithmusgesetze
Exponential- und Logarithmusgleichungen
Definitions- und Wertebereich
Schnittpunkte mit den Koordinatenachsen
Polynomdivision
Newton-Verfahren
Satz vom Nullprodukt
lineare Transformationen von Funktionsgraphen: Spiegeln, Verschieben, Strecken / Stauchen
Achsen- und Punktsymmetrie von Funktionsgraphen
Grenzwertverhalten von Polynomen
senkrechte, waagrechte und schräge Asymptoten
Polstellen mit und ohne Vorzeichenwechsel
Stetig hebbare Definitionslücken
Stetigkeit von Funktionen
Funktionsscharen und Ortslinien von Extrem- und Wendepunkten
Bogenlänge- und Bogenmaß
Differenzenquotient und geometrische Deutung (Bezug zur Sekantensteigung)
Differenzenquotient und mittlere Änderungsrate (auch im Sachzusammenhang)
h-Methode
Differentialquotient
Deutung des Differentialquotienten als Tangentensteigung
Begriff der Differenzierbarkeit von Funktionen
Interpretation als lokale Änderungsrate (auch im Sachzusammenhang)
Aufstellen der Tangenten- und Normalengleichung
Differenzieren einer Funktion
Faktor-, Summen-, Produkt- und Quotinentenregel für das Differenzieren
Rüchschluss von der Ableitung auf das Monotonieverhalten sowie auf Extremwerte
Monotonie der ersten Ableitung
zweite Ableitung und Bestimmung von Krümmungsverhalten und Wendepunkten
Unterscheidung von hinreichenden und notwendigen Bedingungen für die Bestimmung von Extrema und Wendepunkten
Gleichung der Wendetangente
Ableiten des Verlaufs des Graphens einer Stammfunktion aus einer gegebenen Funktion
Bestimmung des Funktionsterms einer Stammfunktion aus dem Term einer gegebenen ganzrationalen Funktion
Differenzieren und Analysieren von Sinus- und Cosinusfunktionen
Verknüpfungen von Sinus- und Cosinus mit ganzrationalen Funktionen untersuchen
Produkt- und Kettenregel für das Differenzieren
Anwenden der Methoden der Differential- und Integralrechnung auf Sinus- und Cosinusfunktionen
Differenzieren und Analysieren von Potenzfunktionen mit negativem ganzzahlingen Exponenten
Differenzieren von einfachen gebrochen-rationalen Funktionen (Grad des Zähler- und Nennerpolynoms ≤2)
Quotientenregel
Anwenden der Methoden der Differential- und Integralrechnung auf gebrochen-rationale Funktionen
Verhalten gebrochen-rationaler Funktionen an den Rändern des Definitionsbereiches
Folgern der Umkehrbarkeit einer Funktion aus der Eigenschaft der strengen Monotonie
Zusammenhang der Graphen von Funktion und Umkehrfunktion
Bestimmung des Funktionsterms der Umkehrfunktion einer gegebenen Funktion (in einfachen Fällen)
Differenzieren der Wurzelfunktion (sowie deren Verknüpfungen und Verkettungen)
Differenzieren und Analysieren der e-Funktion
Anwenden der Methoden der Differential- und Integralrechnung auf e-Funktionen
Grenzwertbestimmung durch Vergleich des Wachstums von Exponential- und Potenzfunktionen
ln-Funktion als Umkehrfunktion der e-Funktion
Differenzieren der natürlichen Logarithmusfunktion
Anwenden der Methoden der Differential- und Integralrechnung auf ln-Funktionen
Grenzwertbestimmung durch Vergleich des Wachstums von Logarithmus- und Potenzfunktionen
Streifenmethode
Definition des Integrals und Hauptsatz der Differential- und Integralrechnung
Bestimmtes Integral und Flächenbilanz
Interpretation des Integrals als Gesamtänderung einer Größe (Integrandenfunktion zeigt lokale Änderungsrate)
Differenzieren und Integrieren als Umkehroperationen
Faktor- und Summenregel für Integrale
Ermitteln von Werten bestimmter Integrale mithilfe von Stammfunktionen
Abgrenzung der Integralfunktion von der Stammfunktion
Berechnung der Fläche zwischen Graph und Koordinatenachse
Berechnung der Fläche zwischen zwei Graphen
Aus dem Verlauf einer Funktion den Verlauf der zugehörenden Integrandenfunktion ableiten und umgekehrt
Volumina von Rotationskörpern
Erkennen und Integrieren von Funktionen der Form f(ax+b) und f´(x)exp(f(x))
Umgang mit unbestimmten Integralen
Ins Unendliche reichende Flächen
Kurvendiskussion
Interpretation von Ergebnissen im Sachzusammenhang
Anwendung dieser Methoden auf inner- und außermathematische Kontexte
Extremwertprobleme
Modellierungen mit Funktionen (Weitsprung, Wurf, Hang,…)
Modelle von exponentiellen, linearen und logistischen Wachstumsprozessen
Abklingprozesse
Funktionsterm aus gegebenen Bedinungen bestimmen (Steckbriefaufgaben)
Bestimmung eines Bestands aus einer gegebenen Änderungsrate
Ergebnis und Ergebnismenge
Ereignis und Gegenereignis
Baumdiagramm und Pfadregeln
Vierfeldertafel
Additionssatz für Wahrscheinlichkeiten
Schnittmenge und Vereinigungsmenge (De Morgansche Gesetze)
Bedingte Wahrscheinlichkeit
Laplace Experimente
Wahrscheinlichkeit als Stabilisierung der relativen Häufigkeit
Axiomatische Definition von Wahrscheinlichkeit nach Kolmogorov
Verknüpfte Ereignisse und ihre Wahrscheinlichkeiten
Abhängigkeit und Unabhängigkeit von Ereignissen
Unmögliche, unvereinbare und sichere Ereignisse
faires Spiel
Zufallsgrößen
Wahrscheinlichkeitsverteilung
Erwartungswerte
Standardabweichung
Varianz
Veranschaulichung der Wahrscheinlichkeitsverteilung durch Säulendiagramme oder Histogramme (d=1)
Zurückführen von Sachsituationen auf das Urnenmodell durch Analogiebildung
Binomialkoeffizient
Binomialverteilung
Berechnung von Wahrscheinlichkeiten, Erwartungswert und Standardabweichung binomial verteilter Größen
Kumulierte Binomialverteilung
dreimal-mindestens-Aufgaben
Hypergeometrische Verteilung (Lotto)
Bernoulliketten
Galtonbrett
grundsätzliches Vorgehen bei links- und rechtsseitigen Signifikanztests
einseitiger Signifikanztest bei als binomialverteilt angenommenen Merkmalen (links- und rechtsseitig)
Abgrenzung der Wahrscheinlichkeitsrechnung von der Statistik
Zielsetzung und Wahl der Nullhypoteste bei Signifikanztests
Entscheidungsregeln und Ablehnungsbereich
Annahme / Verwurf der Nullhypothese
Bestimmung des Ablehungsbereichs des einseitigen Signifikanztests bei gegebenem Signifikanzniveau
Fehler 1. Art und Fehler 2. Art ( = alpha- und beta-Fehler)
Berechnung der Wahrscheinlichkeiten der Fehler 1. und 2. Art
Einfluss des Stichprobenumfangs auf die beiden Fehlerwahrscheinlichkeiten berechen
Bedeutung der Fehler 1. und 2. Art im Sachzusammenhang
Widerlegen von Fehlinterpretationen
Erläuterung der Gaußschen Funktion
Beschreibung des Verlaufs und der charakteristischen Eigenschaften der Integralfunktion der Gaußfunktion
Bedeutung der Parameter μ und σ für den Verlauf des Graphen der Gaußfunktion
Bestimmen von Wahrscheinlichkeiten unter Verwenden der Integralfunktion
Abschätzung der Wahrscheinlichkeiten mit Hilfe der σ-Regeln
Achtung: Nicht Bundeslandunspezifisch! Downloade die passende Checkliste für dein Mathe-Abi hier
Wir bieten dieses Angebot sowie auch weitere Lernhilfen für das Abitur kostenlos an.
Alle SchülerInnen die ein Survival Kit besitzen, oder sich dieses für die Oberstufenzeit und Abiturvorbereitung anschaffen wollen, können beispielsweise auch an unseren Back2School Kursen in jedem Jahr kostenfrei teilnehmen.
Das Fachteam um Paul Bergold, unser Chief Mathmatics Officer, Co-Founder und Doktor der Mathematik (TU München) hat auf der Basis der Lehrpläne sowie einer ausführlichen Analyse der Abituraufgaben der letzten Jahre haben für Dich alle Themen herausgearbeitet, die für eine erfolgreiche Abiturvorbereitung im Fach Mathematik wichtig sind.
Hierbei gehen wir über die Bildungspläne bzw. das Kerncurriculum gymnasiale Oberstufe für Mathematik („Lehrplan“) hinaus und nutzen unser Wissen aus den intensiven Recherchen, Analysen und über 5 Jahre Erfahrung mit der Vorbereitung auf das Mathe-Abi. Aus diesem Grund findest du auch die Grundlagen (meist noch aus der Mittelstufe) für Analaysis, Linearer Algebra/Geomterie und Stochastik, da wir überzeugt davon sind, dass diese einer der entschiedensten Gründe ist, warum SchülerInnen gravierende Schwierigkeiten mit den Oberstufenthemen Mathematik haben.
98% der TeilnehmerInnen würden ABIcrash ihren MitschülerInnen und FreundInnen weiterempfehlen.
95% der ABIcrash TeilnehmerInnen haben ihre zum Ziel gesetzte Abiturnote erreicht oder sogar übertroffen.
100% der KursleiterInnen wurden von den SchülernInnen für ein sehr angenehmes Arbeitsklima gelobt.
ABIcrash – Ein Projekt der MARBA GmbH
Wir vereinbaren auf Wunsch telefonische Beratungstermine: Hier Anfrage senden.
Impressum – Datenschutz – AGB
| Cookie | Dauer | Beschreibung |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |

Melde dich jetzt zu unserem Kursangebot „Back2School“ nach den Sommerferien an! Starte mit guten Noten und überzeuge deine LehrerInnen! Geeignet für die Abiturjahrgänge 2024 und 2025.
Dieser Kurs ist kostenlos für alle BesitzerInnen eines ABIcrash Survival Kits!